Exploiting disorder to probe spin and energy hydrodynamics
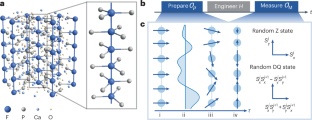
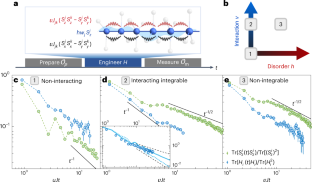
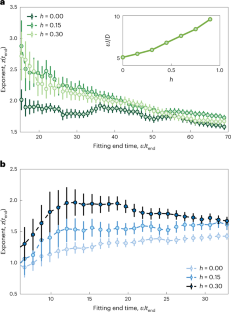
An outstanding challenge in large-scale quantum platforms is to simultaneously achieve strong interactions, giving rise to the most interesting behaviours, and local addressing, which can probe them. In the context of correlated phases, local addressing allows one to directly probe the nature of the system’s order. At the same time, such addressing allows the study of quantum information spreading and operator growth in out-of-equilibrium scenarios. Here we introduce a technique that enables the measurement of local correlation functions, down to single-site resolution, despite access to only global controls. Our approach leverages the intrinsic disorder present in a solid-state spin ensemble to dephase the non-local components of the correlation function. Utilizing this toolset, we measure both the spin and energy transport in nuclear spin chains. By tuning the interaction Hamiltonian via Floquet engineering, we investigate the cross-over between ballistic and diffusive hydrodynamics. Interestingly, in certain parameter regimes, we observe the coexistence of diffusive spin transport with ballistic energy transport, a hallmark of interacting integrable systems.
This is a preview of subscription content, access via your institution
Access options
Access Nature and 54 other Nature Portfolio journals
Get Nature+, our best-value online-access subscription
cancel any time
Subscribe to this journal
Receive 12 print issues and online access
265,23 € per year
only 22,10 € per issue
Buy this article
- Purchase on SpringerLink
- Instant access to full article PDF
Prices may be subject to local taxes which are calculated during checkout

Similar content being viewed by others

Emergent hydrodynamics in a strongly interacting dipolar spin ensemble
Article 01 September 2021
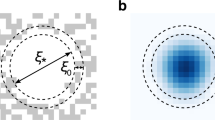
Correlation holes and slow dynamics induced by fractional statistics in gapped quantum spin liquids
Article Open access 05 March 2021
Spin transport in a tunable Heisenberg model realized with ultracold atoms
Article 16 December 2020
Data availability
Source data are provided with this paper. All other data that support the plots within this paper and other findings of this study are available from the corresponding author upon reasonable request.
References
- Halliwell, J. Decoherent histories and the emergent classicality of local densities. Phys. Rev. Lett.83, 2481–2485 (1999). MathSciNetMATHADSGoogle Scholar
- Wyatt, R. E. Quantum Dynamics with Trajectories: Introduction to Quantum Hydrodynamics Vol. 28 (Springer Science & Business Media, 2005).
- Hartle, J. B. The quasiclassical realms of this quantum universe. Found. Phys.41, 982–1006 (2011). MathSciNetMATHADSGoogle Scholar
- Spohn, H. Large Scale Dynamics of Interacting Particles (Springer Science & Business Media, 2012).
- Birkhoff, G. in Hydrodynamics (Princeton University Press, 2015).
- De Nardis, J., Bernard, D. & Doyon, B. Hydrodynamic diffusion in integrable systems. Phys. Rev. Lett.121, 160603 (2018). MathSciNetGoogle Scholar
- Andreev, A., Kivelson, S. A. & Spivak, B. Hydrodynamic description of transport in strongly correlated electron systems. Phys. Rev. Lett.106, 256804 (2011). ADSGoogle Scholar
- Žnidarič, M., Scardicchio, A. & Varma, V. K. Diffusive and subdiffusive spin transport in the ergodic phase of a many-body localizable system. Phys. Rev. Lett.117, 040601 (2016). ADSGoogle Scholar
- Bertini, B., Collura, M., De Nardis, J. & Fagotti, M. Transport in out-of-equilibrium x x z chains: exact profiles of charges and currents. Phys. Rev. Lett.117, 207201 (2016). ADSGoogle Scholar
- Leviatan, E., Pollmann, F., Bardarson, J. H., Huse, D. A. & Altman, E. Quantum thermalization dynamics with matrix-product states. Preprint at arXiv:1702.08894 (2017).
- Ye, B., Machado, F., White, C. D., Mong, R. S. & Yao, N. Y. Emergent hydrodynamics in nonequilibrium quantum systems. Phys. Rev. Lett.125, 030601 (2020). ADSGoogle Scholar
- Ljubotina, M., Žnidarič, M. & Prosen, T. Kardar-Parisi-Zhang physics in the quantum Heisenberg magnet. Phys. Rev. Lett.122, 210602 (2019). ADSGoogle Scholar
- Ye, B., Machado, F., Kemp, J., Hutson, R. B. & Yao, N. Y. Universal Kardar-Parisi-Zhang dynamics in integrable quantum systems. Phys. Rev. Lett.129, 230602 (2022). MathSciNetADSGoogle Scholar
- Sommer, A., Ku, M., Roati, G. & Zwierlein, M. W. Universal spin transport in a strongly interacting Fermi gas. Nature472, 201–204 (2011). ADSGoogle Scholar
- Moll, P. J., Kushwaha, P., Nandi, N., Schmidt, B. & Mackenzie, A. P. Evidence for hydrodynamic electron flow in PdCoO2. Science351, 1061–1064 (2016). ADSGoogle Scholar
- Cepellotti, A. et al. Phonon hydrodynamics in two-dimensional materials. Nat. Commun.6, 6400 (2015). ADSGoogle Scholar
- Crossno, J. et al. Observation of the dirac fluid and the breakdown of the wiedemann-franz law in graphene. Science351, 1058–1061 (2016). ADSGoogle Scholar
- Agarwal, K., Gopalakrishnan, S., Knap, M., Müller, M. & Demler, E. Anomalous diffusion and griffiths effects near the many-body localization transition. Phys. Rev. Lett.114, 160401 (2015). ADSGoogle Scholar
- Castro-Alvaredo, O. A., Doyon, B. & Yoshimura, T. Emergent hydrodynamics in integrable quantum systems out of equilibrium. Phys. Rev. X6, 041065 (2016). Google Scholar
- Bertini, B. Finite-temperature transport in one-dimensional quantum lattice models. Rev. Mod. Phys.93, 025003 (2021). MathSciNetADSGoogle Scholar
- Ilievski, E. & De Nardis, J. Microscopic origin of ideal conductivity in integrable quantum models. Phys. Rev. Lett.119, 020602 (2017). ADSGoogle Scholar
- Gopalakrishnan, S. & Vasseur, R. Kinetic theory of spin diffusion and superdiffusion in x x z spin chains. Phys. Rev. Lett.122, 127202 (2019). ADSGoogle Scholar
- De Nardis, J., Bernard, D. & Doyon, B. Diffusion in generalized hydrodynamics and quasiparticle scattering. SciPost Phys6, 049 (2019). MathSciNetADSGoogle Scholar
- Ilievski, E., De Nardis, J., Gopalakrishnan, S., Vasseur, R. & Ware, B. Superuniversality of superdiffusion. Phys. Rev. X11, 031023 (2021). Google Scholar
- De Nardis, J., Gopalakrishnan, S., Vasseur, R. & Ware, B. Stability of superdiffusion in nearly integrable spin chains. Phys. Rev. Lett.127, 057201 (2021). MathSciNetADSGoogle Scholar
- Friedman, A. J., Gopalakrishnan, S. & Vasseur, R. Diffusive hydrodynamics from integrability breaking. Phys. Rev. B101, 180302 (2020). ADSGoogle Scholar
- Schemmer, M., Bouchoule, I., Doyon, B. & Dubail, J. Generalized hydrodynamics on an atom chip. Phys. Rev. Lett.122, 090601 (2019). ADSGoogle Scholar
- Zu, C. et al. Emergent hydrodynamics in a strongly interacting dipolar spin ensemble. Nature597, 45–50 (2021). ADSGoogle Scholar
- Malvania, N. et al. Generalized hydrodynamics in strongly interacting 1d bose gases. Science373, 1129–1133 (2021). MathSciNetMATHADSGoogle Scholar
- Wei, D. et al. Quantum gas microscopy of Kardar-Parisi-Zhang superdiffusion. Science376, 716–720 (2022). ADSGoogle Scholar
- Joshi, M. K. et al. Observing emergent hydrodynamics in a long-range quantum magnet. Science376, 720–724 (2022). ADSGoogle Scholar
- Martin, L. S. et al. Controlling local thermalization dynamics in a Floquet-engineered dipolar ensemble. Preprint at arXiv:2209.09297 (2022).
- Altman, E. et al. Quantum simulators: architectures and opportunities. PRX Quantum2, 017003 (2021). Google Scholar
- Bakr, W. S., Gillen, J. I., Peng, A., Folling, S. & Greiner, M. A quantum gas microscope for detecting single atoms in a Hubbard-regime optical lattice. Nature462, 74–77 (2009). ADSGoogle Scholar
- Zhang, W. & Cory, D. First direct measurement of the spin diffusion rate in a homogenous solid. Phys. Rev. Lett.80, 1324 (1998). ADSGoogle Scholar
- Rittweger, E., Han, K. Y., Irvine, S. E., Eggeling, C. & Hell, S. W. STED microscopy reveals crystal colour centres with nanometric resolution. Nat. Photonics3, 144–147 (2009). ADSGoogle Scholar
- Maurer, P. et al. Far-field optical imaging and manipulation of individual spins with nanoscale resolution. Nat. Phys.6, 912–918 (2010). Google Scholar
- Chen, E. H., Gaathon, O., Trusheim, M. E. & Englund, D. Wide-field multispectral super-resolution imaging using spin-dependent fluorescence in nanodiamonds. Nano Lett.13, 2073–2077 (2013). ADSGoogle Scholar
- Pfender, M., Aslam, N., Waldherr, G., Neumann, P. & Wrachtrup, J. Single-spin stochastic optical reconstruction microscopy. Proc. Natl Acad. Sci. USA111, 14669–14674 (2014). ADSGoogle Scholar
- Arai, K. et al. Fourier magnetic imaging with nanoscale resolution and compressed sensing speed-up using electronic spins in diamond. Nat. Nanotechnol.10, 859–864 (2015). ADSGoogle Scholar
- Hunt, G. A. Some theorems concerning brownian motion. Trans. Am. Math. Soc.81, 294–319 (1956). MathSciNetMATHGoogle Scholar
- Waugh, J. S., Huber, L. M. & Haeberlen, U. Approach to high-resolution nmr in solids. Phys. Rev. Lett.20, 180–182 (1968). ADSGoogle Scholar
- Jeener, J. & Broekaert, P. Nuclear magnetic resonance in solids: thermodynamic effects of a pair of rf pulses. Phys. Rev.157, 232–240 (1967). ADSGoogle Scholar
- Haeberlen, U. & Waugh, J. S. Coherent averaging effects in magnetic resonance. Phys. Rev.175, 453–467 (1968). ADSGoogle Scholar
- Peng, P. et al. Deep reinforcement learning for quantum hamiltonian engineering. Phys. Rev. Appl.18, 024033 (2022). ADSGoogle Scholar
- Grabowski, M. & Mathieu, P. Structure of the conservation laws in quantum integrable spin chains with short range interactions. Ann. Phys.243, 299–371 (1995). MathSciNetMATHADSGoogle Scholar
- Zotos, X., Naef, F. & Prelovsek, P. Transport and conservation laws. Phys. Rev. B55, 11029–11032 (1997). ADSGoogle Scholar
- Klümper, A. & Johnston, D. Thermodynamics of the spin-1/2 antiferromagnetic uniform Heisenberg chain. Phys. Rev. Lett.84, 4701–4704 (2000). ADSGoogle Scholar
- Sakai, K. & Klümper, A. Non-dissipative thermal transport in the massive regimes of the xxz chain. J. Phys. A: Math. Gen.36, 11617–11629 (2003). MathSciNetMATHADSGoogle Scholar
- Prosen, T. & Žnidarič, M. Matrix product simulations of non-equilibrium steady states of quantum spin chains. J. Stat. Mech.: Theory Exp.2009, P02035 (2009). Google Scholar
- Steinigeweg, R. & Gemmer, J. Density dynamics in translationally invariant spin-1 2 chains at high temperatures: a current-autocorrelation approach to finite time and length scales. Phys. Rev. B80, 184402 (2009). ADSGoogle Scholar
- Žnidarič, M. Spin transport in a one-dimensional anisotropic Heisenberg model. Phys. Rev. Lett.106, 220601 (2011). ADSGoogle Scholar
- Karrasch, C., Moore, J. & Heidrich-Meisner, F. Real-time and real-space spin and energy dynamics in one-dimensional spin-1 2 systems induced by local quantum quenches at finite temperatures. Phys. Rev. B89, 075139 (2014). ADSGoogle Scholar
- Lucioni, E. et al. Observation of subdiffusion in a disordered interacting system. Phys. Rev. Lett.106, 230403 (2011). ADSGoogle Scholar
- Vosk, R., Huse, D. A. & Altman, E. Theory of the many-body localization transition in one-dimensional systems. Phys. Rev. X5, 031032 (2015). Google Scholar
- Potter, A. C., Vasseur, R. & Parameswaran, S. Universal properties of many-body delocalization transitions. Phys. Rev. X5, 031033 (2015). Google Scholar
- Sahay, R., Machado, F., Ye, B., Laumann, C. R. & Yao, N. Y. Emergent ergodicity at the transition between many-body localized phases. Phys. Rev. Lett.126, 100604 (2021). ADSGoogle Scholar
- Zaburdaev, V., Denisov, S. & Klafter, J. Lévy walks. Rev. Mod. Phys.87, 483–530 (2015). ADSGoogle Scholar
- Nahum, A., Vijay, S. & Haah, J. Operator spreading in random unitary circuits. Phys. Rev. X8, 021014 (2018). Google Scholar
- Von Keyserlingk, C., Rakovszky, T., Pollmann, F. & Sondhi, S. L. Operator hydrodynamics, OTOCs, and entanglement growth in systems without conservation laws. Phys. Rev. X8, 021013 (2018). Google Scholar
- Rakovszky, T. & Pollmann, F. & Von Keyserlingk, C. Diffusive hydrodynamics of out-of-time-ordered correlators with charge conservation. Phys. Rev. X8, 031058 (2018). Google Scholar
- Khemani, V., Vishwanath, A. & Huse, D. A. Operator spreading and the emergence of dissipative hydrodynamics under unitary evolution with conservation laws. Phys. Rev. X8, 031057 (2018). Google Scholar
- Xu, S. & Swingle, B. Accessing scrambling using matrix product operators. Nat. Phys.16, 199–204 (2020). Google Scholar
- Xu, S. & Swingle, B. Locality, quantum fluctuations, and scrambling. Phys. Rev. X9, 031048 (2019). Google Scholar
- Sahu, S., Xu, S. & Swingle, B. Scrambling dynamics across a thermalization-localization quantum phase transition. Phys. Rev. Lett.123, 165902 (2019). ADSGoogle Scholar
- Schuster, T. et al. Many-body quantum teleportation via operator spreading in the traversable wormhole protocol. Phys. Rev. X12, 031013 (2022). Google Scholar
- Li, J. et al. Measuring out-of-time-order correlators on a nuclear magnetic resonance quantum simulator. Phys. Rev. X7, 031011 (2017). ADSGoogle Scholar
- Landsman, K. A. et al. Verified quantum information scrambling. Nature567, 61–65 (2019). ADSGoogle Scholar
- Blok, M. S. et al. Quantum information scrambling on a superconducting qutrit processor. Phys. Rev. X11, 021010 (2021). Google Scholar
- Wei, K. X. et al. Emergent prethermalization signatures in out-of-time ordered correlations. Phys. Rev. Lett.123, 090605 (2019). ADSGoogle Scholar
- Cappellaro, P., Ramanathan, C. & Cory, D. G. Simulations of information transport in spin chains. Phys. Rev. Lett.99, 250506 (2007). ADSGoogle Scholar
- Cappellaro, P., Viola, L. & Ramanathan, C. Coherent-state transfer via highly mixed quantum spin chains. Phys. Rev. A83, 032304 (2011). ADSGoogle Scholar
- Ramanathan, C., Cappellaro, P., Viola, L. & Cory, D. G. Experimental characterization of coherent magnetization transport in a one-dimensional spin system. New J. Phys.13, 103015 (2011). ADSGoogle Scholar
- Rufeil-Fiori, E., Sánchez, C. M., Oliva, F. Y., Pastawski, H. M. & Levstein, P. R. Effective one-body dynamics in multiple-quantum nmr experiments. Phys. Rev. A79, 032324 (2009). ADSGoogle Scholar
- Zhang, W. et al. NMR multiple quantum coherences in quasi-one-dimensional spin systems: comparison with ideal spin-chain dynamics. Phys. Rev. A80, 052323 (2009). ADSGoogle Scholar
- Comodi, P., Liu, Y., Zanazzi, P. & Montagnoli, M. Structural and vibrational behaviour of fluorapatite with pressure. Part I: in situ single-crystal x-ray diffraction investigation. Phys. Chem. Miner.28, 219–224 (2001). ADSGoogle Scholar
Acknowledgements
We thank C. Ramanathan, H. Zhou, M. Leigh, N. Leitao, F. Machado, J. Kemp, J. Moore and M. Lukin for helpful conversations. This work was supported in part by the National Science Foundation under grant No. PHY1915218. P.P. thanks MathWorks for their support in the form of a Graduate Student Fellowship. The opinions and views expressed in this publication are from the authors and not necessarily from MathWorks. B.Y. acknowledges support from the Army Research Office through the MURI program (W911NF-20-1-0136). N.Y.Y. acknowledges support from the NSF through the QLCI program (OMA-2016245) and the David and Lucile Packard foundation.
Author information
- These authors contributed equally: Pai Peng, Bingtian Ye.
Authors and Affiliations
- Department of Electrical Engineering and Computer Science, Massachusetts Institute of Technology, Cambridge, MA, USA Pai Peng
- Department of Physics, University of California, Berkeley, CA, USA Bingtian Ye & Norman Y. Yao
- Department of Physics, Harvard University, Cambridge, MA, USA Bingtian Ye & Norman Y. Yao
- Department of Nuclear Science and Engineering, Massachusetts Institute of Technology, Cambridge, MA, USA Paola Cappellaro
- Research Laboratory of Electronics, Massachusetts Institute of Technology, Cambridge, MA, USA Paola Cappellaro
- Pai Peng








